 CUCaTS
Puzzlehunt 2017
CUCaTS
Puzzlehunt 2017
ronscode.com
<!DOCTYPE html> <html> <head><title>Ron's page</title></head> <body> <p> Hi, I'm Ron and I've written lots of software. Please take a look at <a id="v4">ronscode.com</a>. </p> <script type="text/javascript"> // I don't want people scraping this off my website so I used version // 13 of the algorithm made by me, Prof. O and Dr T to encrypt it. It's // *SUPER* secure and I always make sure to encrypt data in my programs. var url = [ 'qngn:nccyvpngvba/bpgrg-fgernz;onfr64,6kqtXpiih+u1UZAlf0W7SFDSHYDP', 'mFSLjmUovM/4Ni7QtCfNqsHk/mUoZsLkjNB/+NXXuNVOOVNOk4Ua/jPXu/tPvdK4N', 'bva+NXVustPEhyINMRl3EfU8PIEfuOHA+OIRayhaZ+qe3XbF/vKqIskLTH7vbKqyQ', '+lR1X4JJuJx0so5QnT052NfyJljMpHxkH61PXRVb78lYWmnqgDRXT7NcmAatu1RBz', 'oWUQwhNI3hKbP3iMCBCRFg+6MqOpeMCcezh8eqoS2ACQi4FTJ+ic0i4Lc1UgGIAG+', 'WUzdFqacenj0WHrVa/JFOF5JrCIxi66kHhBbkzyCU+MQWwtbeKnX7bI1LCdp3JXgq', 'J7XTdcbTRMupSK4K5m8xdMVNPZKdEXoBZZeIcjjp/MPCkmE8ADeFDXFrDjoO1WWBE', 'KLnQOcUvruLzthQ6ZztBT44/BrmhZfNE4ADr9BR/hZCPS98lqeJlVPSudEIamc6z7', 'c51rD09vc/uHmPSBHVHAkfpX1mBSbpowk0owUbE6IgOOfTNNcdCJE1ix2vMlva05K', 'IQYjv3Hg1GgGnHD3t+LCD4Q7NN+SsC4k2mU2Zs9Ttro/NNB8+NXO5/8NvbG4Nbdy+', 'NXVcCtPvVK4NyZk24dp+NVPastPvcs4Nyfly1VO6Po+D4U7IDS8kotNGZ0u', ].join(''); // Polyfill until browsers implement this natively. // (credit: Jonas Raoni Soares Silva) String.prototype.decrypt = function(){ return this.replace(/[a-zA-Z]/g, function(c){ return String.fromCharCode( (c <= "Z" ? 90 : 122) >= (c = c.charCodeAt(0) + 13) ? c : c - 26); }); }; var e = document.getElementById('v4'); e.setAttribute('href', url.decrypt()); e.setAttribute('download', e.textContent); </script> </body> </html>
Solution
author: Rich Wareham (rjw57)
The puzzle is presented as some HTML source to a website. It looks to be an advert pointing to Ron's personal code hosting site at http://ronscode.com.
The page is quite odd in that Ron appears to be very protective of his code
hosting site and has attempted to encrypt the link. The page includes code to
decrypt the link and "display" it in the href attribute of the <a> tag.
The <a> tag's id is "v4". Perhaps this is version 4 of ronscode.com?
The link is encrypted using the ROT13 algorithm. Ron claims in his comment that this is version 13 of the algorithm developed in association with his colleagues whose surnames begin with "O" and "T". This suggests the following:
- Ron invents encryption algorithms.
- Ron names things at the initials of the creators followed by a version number.
- Ron's surname begins with "R" (to make "ROT13").
Those with a cryptographic bent may already have identified Ron but a Google for "Ron's code" and the number 4 will turn up the interesting fact that the RC4 stream cipher is so named because it is "Ron's Code" version 4. The Ron in questions being Ron Rivest the founder/inventor of RSA. ("RSA" itself being an initialism formed from the surnames of Ron and his co-founders.)
We now know who Ron is and maybe have a clue that RC4 may be being used somewhere rather than the somewhat less effective ROT13.
Clicking on the ronscode.com link does not lead to a website. Instead it's a
file which gets downloaded.
At this point there are several ways in which the solution can proceed. One
might make the leap of judgement that ronscode.com is an RC4 encrypted
message. The binary file does indeed contain a RC4 encrypted message but the key
is obfuscated so a brute force approach of trying to decrypt the file at various
offsets using key extracted from other offsets would not work. The key is
obfuscated with "ROT128" so perhaps someone making truly astonishing leaps of
logic might correlate ROT13 for text with ROT128 for binary data but that seems
unlikely.
The intended progression is that people realise that the initial part of the
puzzle was intended to put web technologies into the mind of the solver. This is
done so that the solver be guided away from spending effort thinking of other
meanings for the .com suffix. Those with long memories or access to Google
might recall that the COM file format is an executable format used
by DOS.
Indeed ronscode.com is not a website; it is a DOS-style 8.3 filename. Those
enterprising enough to load the file in dosbox will
see a secret message:
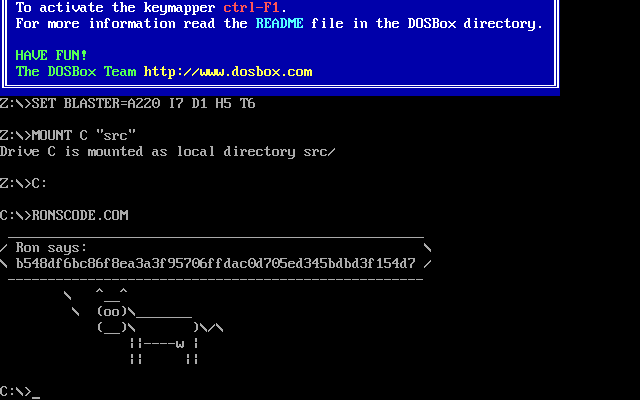
(The exact message will depend on the build of ronscode.com. The key changes with each build. Reproducable builds? Pshaw!)
Again there are multiple ways to proceed from this point. One can reverse
engineer the binary to see how it manages to print out the message despite the
message not being in the source. Those adept at reading 16-bit Intel disassembly
will see that the binary implements an RC4 decoder and simply prints the
plaintext message using the ciphertext and key embedded in the binary. (The key
is obfuscated with ROT128 and included at the top of the file to be evil and
stop the file utility from recognising ronscode.com as a DOS
executable.)
Ron appears to have a taste for writing self decrypting code. The Javascript
implementation of ROT13 is intended as a clue to indicate how ronscode.com
functions as something which decrypts a ciphertext and displays it. Indeed, the
key in ronscode.com is obfuscated with ROT128 so Ron's taste for ROTx
algorithms shows itself again.
The message which Ron says is a hex encoded ciphertext encrypted with the same
key as the cowsay message. It decodes to "What city was I born in?". Knowing
the identity of Ron it's easy to look up Ron Rivest's wikipedia page and
discover that he was born in Schenectady, New York.
A more sophisticated attacker being unwilling to reverse engineer the binary to
find the key may attempt a "known plaintext" attack by assuming that Ron's
message is encrypted with the same key as the cowsay message which handily
contains a large amount of known plaintext at the beginning. The following
Python script attempts a known plaintext attack by iterating through each
possible offset within ronscode.com looking for the ciphertext. It assumes
that the message will be ASCII and uses this to reject invalid matches. It so
happens that there's only one match and that match reveals the correct
plaintext.
It's hoped that the known plaintext attack is encouraged by hiding the key within the binary and obfuscating it with ROT128.
#!/usr/bin/env python3 import os # Change to the directory holding this script. On my system I've saved some # files in a '../src' directory relative to this script. os.chdir(os.path.dirname(os.path.realpath(__file__))) # Read in the binary which we hope contains ciphertext 1 at some offset. with open('ronscode.com', 'rb') as f: ct1 = f.read() # First section of plaintext version of ciphertext 1. There's a reason it's # done with cowsay. It makes typing this in easy! pt1 = b' _______________________________________' # Read in what Ron says. with open('ronsays.bin', 'rb') as f: ct2 = f.read() # RC4 is a stream cipher. Assuming the same key is used for both ciphertexts # and the keystream is k then # # ct1 = pt1 ^ k, ct2 = pt2 ^ k => ct1 ^ ct2 ^ pt1 = pt2 # # Hence if we exclusive or the two ciphertexts and the known plaintext we can # recover the other plaintext. # We don't know the offset of ciphertext 1 in ronscode.com so we iterate through # all offsets which are valid. for off in range(len(ct1) - len(ct2)): # Form candidate plaintext. pt2 = bytes(c1 ^ c2 ^ p1 for c1, c2, p1 in zip(ct1[off:], ct2, pt1)) # It's a possible match if all plain text bytes are ASCII. if all([b < 128 for b in pt2]): print('Possible match @ {}: {}'.format(off, repr(pt2.decode('ascii'))))